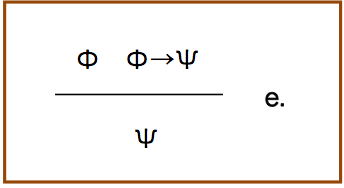
引き続き,推論規則である.最初の例は,以前に出てきた.
原子式の記号が,ギリシャ文字に変わっているが同じである.Φが削除されているので,ここでは単に「e.」規則としている.日本語方式だと,「去-→」である.
ちなみに,「入->」というのは何であろうか.これまで使ってきた演繹そのものを指す.Φ,Ψが真ならばΞであるというときに,Φ,Ψ→Ξ が結論になるような推論規則である.
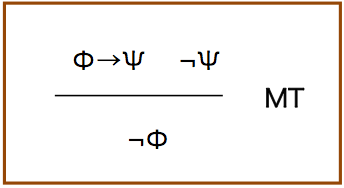
上記は,modus ponens という名前を持つ.これはラテン語で,肯定の方法という意味とのこと(動詞原形のponoは「置く」,tolloは「持ち上げる」というのが基本的な語義だと思う).結論が肯定なのでこの名前がある.否定の方法(modus tollens)というのもあり,以下の形になる.
先と同様に原子式ψが消える.かつ結論は,否定の形式になっている.
真理値表を使って,Φ→Ψが真で,後件が偽の場合というのは前提Φが偽の場合しかないことから分かる(Φが偽だと,Ψの値によらず真になる).或いは,¬Φ ∨ Ψという変形を用いて,¬Ψが真であることから導いても良い.
では,次はどうであろうか.
Φ → Ψ , ¬Φ ⊢ ¬Ψ
前件の否定(Denying the antecedent)と呼ばれる.もちろん正当ではない.「Φ → Ψ」において,前件が偽であれば,後件は真偽の何れでも取り得る.
ここで,→について少し考えてみる.
| Φ | ψ | Φ→ψ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Φ:「雨が降る」
Ψ:「スリップしやすくなる」
このとき,「Φ→Ψ」だとすると,雨が降っていないときには,Ψの真偽によらずに,この式が真になるというのは,どういうことだろうか.
日常会話で,「雨が降っているとスリップしやすいよね」というときに,雨が降っていないときのことを気にしていないか,(相対的に)スリップしにくいと考えている.プログラムに対応させると次にようになるかもしれない.
if PHI then PSI end if;
Φが偽の場合は,そもそもΨは評価対象ではない.
一様の表だが,前件部が偽の場合を考えると,自然言語とプログラムとも異なっていることが分かる.そういうシンボルの体系だということである.
(nil)